인프런 강의 링크: https://inf.run/DuvN7
[지금 무료] 코딩 테스트 합격자 되기 - C++ 강의 | dremdeveloper - 인프런
dremdeveloper | 코딩 테스트 합격을 위한 C++ 강의, 책 없이도 가능! 저자와 직접 소통 가능한 커뮤니티 제공!, [사진]여기에 문의 하세요https://open.kakao.com/o/gX0WnTCf📘 코딩 테스트 합격자 되기 - C++편
www.inflearn.com
2주 차
스터디 일자: (2024. 07. 14(일) ~ 2024. 07. 20(토))
시작에 앞서
1주 차에 배운 시간 복잡도를 알고리즘 풀이에 적용하며 문제를 해결했다
C++은 기초적인 부분을 학습하고 있어서 시간 복잡도가 큰 의미가 없었지만,
Java로 문제를 풀 때에는 어떤 알고리즘을 사용해야 하는지 고민하기 시작했다
예를 들어, 최대 N값이 10억이 주어진 경우, logN 또는 NlogN 이하의 시간 복잡도를 가지고 있는 이진 탐색 등을 사용하며 문제를 해결해 나갔다
스택과 큐에 대해서는 Java에서 정말 많이 사용해 보았다
이번 주에 봤던 기업 코딩테스트 문제 또한 스택을 활용해 해결하는 문제였다
이번 스터디 기회에 C++의 스택 / 큐의 구현을 학습하고, Java에서 스택 / 큐가 어떤 구조를 가지고 있는지 확인해 보고자 한다
이전에 Java에서 ArrayList의 구현체를 뜯어보았을 때, 처음에 약 10의 크기를 가지는 배열이 생성되고
이후에 현재 용량의 절반씩 증가하는 방식이 적용되어 있었다(10 -> 15 -> 22 -> 33...)
// 다른 코드
private static final int DEFAULT_CAPACITY = 10;
// 다른 코드
private Object[] grow(int minCapacity) {
int oldCapacity = elementData.length;
if (oldCapacity > 0 || elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
oldCapacity >> 1 /* preferred growth */);
return elementData = Arrays.copyOf(elementData, newCapacity);
} else {
return elementData = new Object[Math.max(DEFAULT_CAPACITY, minCapacity)];
}
}
// 다른 코드
이번 스터디를 통해 Java 사용하는 스택과 큐의 구조를 좀 더 자세히 파악하고
C++에서 스택과 큐를 구현하고 사용하는 방법을 파악하고자 한다
1. 스택(Stack)
1-1. 스택의 개념
스택은 LIFO(Last In First Out) - FILO(First In Last Out)의 형태를 가지고 있다

우리가 물건을 쌓을 때처럼 먼저 넣는 데이터가 가장 아래로 깔리게 된다
위에 쌓인 데이터들을 치워야 밑에 있는 데이터를 사용할 수 있다
이런 스택 구조는 운영체제나 프로그래밍 기초에서도 등장한다(재귀, 함수 등)
프로세스에 스택 영역은 함수 호출, 로컬 변수 저장, 함수 인자 전달, 반환 주소 저장 등의 역할을 한다
스택에 쌓인 마지막 함수를 처리하며 바로 직전에 호출했던 함수로 계속 돌아가는 구조가 스택의 원리를 활용한 것
우리가 문서 편집이나 프로그래밍할 때 매우 자주 사용하는 Ctrl + z(undo) 기능도 스택을 활용한 방법이다
웹 사이트의 뒤로 가기 또한 스택을 활용한 방식이다
스택을 사용할 때는 Stack Overflow를 조심해야 한다
우리가 재귀를 잘못 사용해서 탈출하지 못하거나, 너무 많은 깊이로 들어가는 경우 해당 오류가 나온다
이는 제한된 스택의 범위를 초과하여 함수 호출 또는 변수 선언 등이 이루어진 경우 발생한다
코딩 테스트 문제를 풀 때, 해당 문제가 스택 문제인지 파악하는 것이 필요하다
1. 가장 최근에 들어온 원소를 알 수 있다
2. 가장 최근에 들어온 원소 순으로 나온다
코딩 테스트 문제를 해결할 때, 가장 최근값을 활용해 비교하고, 연산하는 문제인지 파악해 보면 도움이 될 것이다
참고로, peek은 java의 메서드이고, C++에서는 top 메서드를 통해 최 상단 값을 확인한다
1-2. 스택의 ADT
ADT(Abstract Data Type)?
추상 데이터 타입의 약어로 세부 사항을 숨기고 사용자에게 필요한 기능만 명시한다
우리는 ArrayList, Stack, Queue 등의 자료구조가 어떻게 구성되고, 동적으로 할당되며, 저장 공간을 차지하는지 몰라도 된다
그냥 push, pop, add, size... 등의 메서드만 사용하면 잘 처리해 준다
위에 <시작에 앞서> 부분에서 Java의 ArrayList가 어떻게 배열 크기를 늘리는지를 확인했다
하지만, ArrayList를 사용할 때 저 로직을 몰라도 데이터를 저장하고 빼내는 데 문제가 없는 것과 마찬가지다
하지만, 면접을 위해서는 이런 자료구조에 대해 조금 더 알 필요가 있다
따라서 나는 면접 준비를 위해서(이번에 코딩 테스트 문제가 스택이었는데, 해당 자료 구조에 대해 깊은 질문이 들어올 수 있기 때문에~) 후반부에 Java의 Stack을 조금 까볼 예정이다
C++
| 구분 | 정의 | 설명 |
| 연산 | boolean isFull() | 스택이 maxsize인지 확인 가득 차 있다면 True, 아니면 False |
| boolean isEmpty() | 스택에 데이터가 없으면 True, 있으면 False |
|
| void push(ItemType item) | 스택에 데이터 삽입(푸시) | |
| ItemType pop() | 스택의 Top에 있는 데이터를 스택에서 꺼내며 반환 | |
| 상태 | int top | 스택에 최근 푸시한 데이터의 위치 기록 |
| ItemType data[maxsize] | 스택 데이터를 관리하는 배열 최대 maxsize개의 데이터 관리 |
1-3. 스택의 사용 예시
함수 호출
main 함수부터 차례로 함수를 호출하며 스택에 쌓인다
마지막 호출된 함수의 return부터 뒤로 돌아가며 스택의 위에 있는 함수들을 하나씩 빼온다
Java로 예시 코드를 작성해 보겠다
public class Test {
public static void main(String[] args) {
System.out.println("메인 함수 시작");
call(1);
System.out.println("메인 함수 종료");
}
static void call(int depth) {
if (depth == 5) {
System.out.println(depth + "번 함수 호출, 최대 깊이 도달");
return;
}
System.out.println(depth + "번 함수 호출");
call(depth + 1);
System.out.println(depth + "번 함수 종료");
}
}
메인 함수 시작
1번 함수 호출
2번 함수 호출
3번 함수 호출
4번 함수 호출
5번 함수 호출, 최대 깊이 도달
4번 함수 종료
3번 함수 종료
2번 함수 종료
1번 함수 종료
메인 함수 종료
1. main 함수 시작
2. main → 1번 call 호출
3. 1번 call → 2번 call 호출
4. 2번 call → 3번 call 호출
5. 3번 call → 4번 call 호출
6. 4번 call → 5번 call 호출 → 최대 깊이 5 도달 return 5
7. 5번 call 제거 → 4번 call 복귀(스택의 top) → return 4
8. 4번 call 제거 → 3번 call 복귀 → return 3
9. 3번 call 제거 → 2번 call 복귀 → return 2
10. 2번 call 제거 → 1번 call 복귀 → return 1
11. 1번 call 제거 → main 복귀 → 메인함수 종료
이런 흐름을 가진다
Stack Overflow
그럼 스택은 몇 번 call까지 불러올 수 있을까?
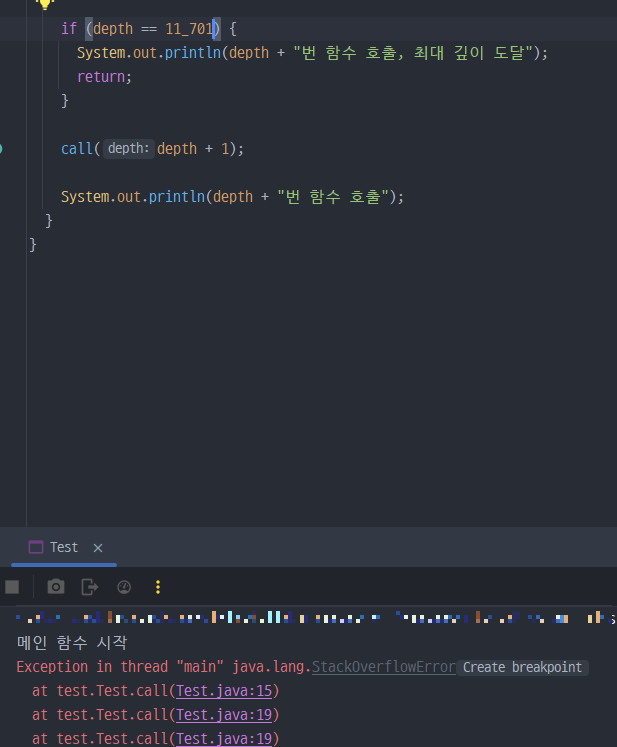
Java 기준으로 강제 overflow를 생성해 테스트를 진행해 보았다
그랬더니, 11,700번 까지는 호출을 성공했으나, 11,701이 되는 순간 stack overflow가 발생했다
따라서 재귀 연산을 11,700번 이상 진행하는 경우 우리는 문제를 해결할 수 없다는 걸 꼭 기억하자

스택 활용 예제
괄호 짝 맞추기는 대표적인 스택 활용 문제이다
보통 문제 해결 방식은 이러하다
1. 열린 괄호 짝은 스택에 삽입한다
2. 닫힌 괄호가 나오면, 스택의 top을 확인한다(peek())
3. 만일 top에 괄호가 이상한 짝이라면(예를 들면, )가 현재 괄호라 top에 (가 있어야 하는데, {가 있는 경우) 올바르지 않다
4. 만일 전체 괄호 점검을 진행했는데 스택에 남은 괄호가 있다면, 짝이 맞지 않으므로 올바르지 않다
이런 방식으로 진행한다
스택을 활용하면 패턴 길이만큼 진행하면 되므로 O(N) 시간 복잡도 내에 해결 가능하다
2. 큐(Queue)
2-1. 큐의 개념
큐는 FIFO(First In First Out), LILO(Last In Last Out) 구조를 가지고 있다
컨베이어 벨트를 생각하면 이해가 쉽다
먼저 넣은 데이터가 컨베이어 벨트의 가장 끝으로 먼저 이동하며, 데이터를 뺄 때는 가장 끝에 도달한 녀석부터 뺀다
현실의 줄 서기가 Queue의 대표적인 예이다
아마 경영학을 전공한 사람들은 생산 관리와 같은 분야에서 매우 많이 들어보았을 것이다
은행 창구 같은 곳은 대기표 번호순으로 들어간다
PriorityQueue와 같이 가중치를 둔 우선순위 큐도 존재한다
놀이공원에서 시즌패스같이 추가 비용을 들여 구매한 사람들이 우선순위가 있는 대기자이다
일반 대기줄에서 나보다 늦게 온 사람이 먼저 들어가는 건 용서할 수가 없다...
하지만 우선순위가 있는 대기줄에서 나보다 늦게 온 사람이 패스권으로 먼저 들어가는 경우는 이해가 된다
우선순위 큐도 매우 많이 사용하므로 지속적인 코딩 테스트 연습이 필요하다
참고로 우선순위 큐는 힙 자료구조를 활용해 구현되며, 이 정렬 과정은 힙 정렬이다
프로세스의 스택 영역처럼 우리 운영체제에서 Queue를 사용하는 경우가 있다
함수, 데이터, 메모리 주소 등은 스택을 통해 관리되지만,
프로세스의 스케줄링(어떤 프로세스를 먼저 수행할 것인가)은 Queue 자료구조를 활용한다
Ready Queue(준비 큐), Waiting Queue(대기 큐)에는 먼저 들어온 요청부터 처리하게 된다
프로세스 간 통신(IPC, Inter-Process Comunication)의 Message Queue(메시지 큐)도 Queue를 활용한 통신 방식이다
운영체제의 System Call(시스템 요청, 시스템 콜) 또한 Queue 방식을 활용해 처리한다
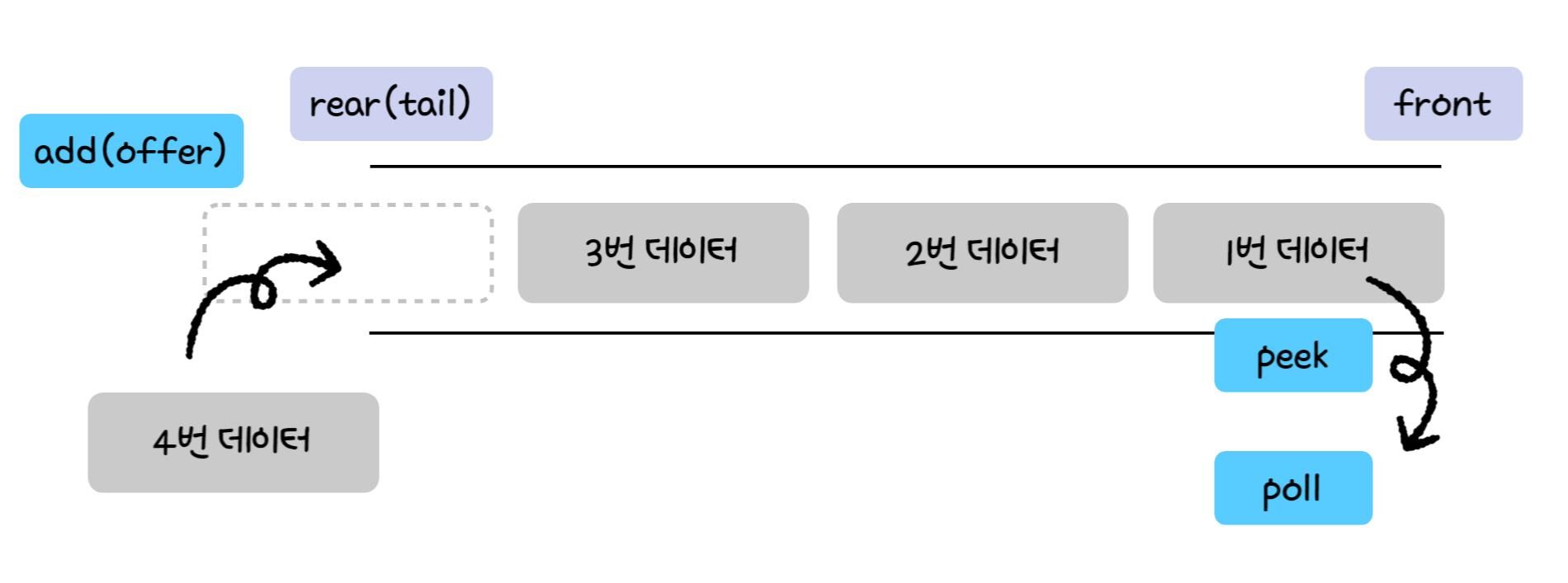
아래 그림에서 출력 방식에 poll을 사용했는데, C++에서는 Stack과 마찬가지로 pop을 사용한다
poll은 자바의 출력 메서드다
입력 방식도 마찬가지로 add 또는 offer는 Java의 입력 방식이다
C++에서는 push를 사용한다
다음 나올 값을 확인하는 메서드도 peek은 java에서, front는 C++에서 활용하는 메서드이다
2-2. 큐의 ADT
Stack과 상당히 유사하다
그러나 Stack은 top만 기록하는 반면, Queue는 rear라는 최근 삽입 값도 저장한다
삽입시에는 front는 고정되고, rear는 변경된다
출력시에는 rear는 고정되고 front는 변경된다
front와 rear가 만나는 경우에 이 Queue에는 아무런 데이터가 남지 않는다
| 구분 | 정의 | 설명 |
| 연산 | boolean isFull() | 큐에 들어있는 데이터 개수가 maxsize인지 확인, 가득 차 있다면 True, 아니면 False |
| boolean isEmpty() | 큐에 데이터가 하나도 없으면 True, 있으면 False | |
| void push(ItemType item) | 큐에 데이터를 삽입(push) | |
| ItemType pop() | 큐에서 front 데이터를 꺼내며 반환(pop) | |
| 상태 | int front | 큐에서 가장 마지막에 pop한 위치 기록 |
| int rear | 큐에서 가장 최근에 삽입된 데이터 위치 기록 | |
| ItemType data[maxsize] | 큐의 데이터를 관리하는 배열 최대 maxsize개의 데이터 관리 |
2-3. 큐의 사용 예시
요세푸스 문제
Stack에 괄호 맞추기가 있다면, Queue에는 요세푸스 문제가 있다
주어진 인원 수 N과 시작 위치 K가 주어진 경우, K번 째 사람을 계속 제거하며 마지막 남는 사람을 찾아내는 문제이다
N은 5, K는 2인 경우(1, 2, 3, 4, 5 사람이 있다)
1. 1을 출력 → 현재 K는 1 → 다시 Queue에 삽입 / Queue Status = (2, 3, 4, 5, 1)
2. 2를 출력 → 현재 K는 2 → 삽입하지 않고 진행 / Queue Status = (3, 4, 5, 1)
3. 3을 출력 → 현재 K는 1 (다시 1부터 진행한다) → 다시 Queue에 삽입 / Queue Status = (4, 5, 1, 3)
4. 4를 출력 → 현재 K는 2 → 삽입하지 않고 진행 / Queue Status = (5, 1, 3)
5. 5를 출력 → 현재 K는 1 → 다시 Queue에 삽입 / Queue Status = (1, 3, 5)
6. 1을 출력 → 현재 K는 2 → 삽입하지 않고 진행 / Queue Status = (3, 5)
7. 3을 출력 → 현재 K는 1 → 다시 Queue에 삽입 / Queue Status = (5, 3)
8. 5를 출력 → 현재 K는 2 → 삽입하지 않고 진행 / Queue Status = (3)
9. Queue의 size가 1이므로, 마지막 남은 3이 정답
참고로 여기서 K를 1, 2, 1, 2, 로 반복하는 것을 mod연산으로 진행하면 편리하다
현재 카운팅 = 1 % K 로 진행하게 되면,
0 % 2 = 0(1번)
1 % 2 = 1(2번)
2 % 2 = 0(1번)
이렇게 반복적인 값을 받아와 활용할 수 있다
이렇게 되면, 나머지 값 + 1일 때가 K번 사람이 되는 것이다
BFS
너비 우선 탐색도 대표적인 Queue를 활용한 방식이다
Queue에 먼저 만나는 데이터를 삽입하며, 연결된 데이터를 다시 Queue에 넣는다
더 이상 연결된 데이터가 없으면, Queue의 front를 출력하여 해당 값과 연결된 노드 데이터들을 또 탐색한다
보통 Stack은 DFS(깊이 우선 탐색)에서 사용하며, Queue는 BFS에서 많이 활용한다
해당 파트는 나중에 그래프 탐색에서 더 다룰 기회가 있을 것이다
참고로 깊이 우선 탐색은 재귀 방식을 더 많이 활용한다(구조는 유사하지만 코드 자체가 깔끔해서 많이 사용한다고 함)
3. 문제 풀이
3-1. 괄호 회전하기
https://school.programmers.co.kr/learn/courses/30/lessons/76502
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
최대한 메서드화 하여 문제를 해결했다
기존 java로 푼 경험이 있어서 접근도 쉬웠다
시간 복잡도를 계산하면, 우선 괄호를 회전하는 경우는 s의 길이 - 1만큼이다( 1 ≤ s ≤ 1,000)
길이가 6이라면 최대 5번 회전, -1은 큰 의미가 없으므로 대략 1,000회라고 계산하자
이후 Stack을 통해 값을 점검하면 N의 선형시간만큼 탐색한다
따라서 괄호 회전 수(N) * 회전한 데이터 탐색 수 (N)으로
O(N2)의 시간이 소요될 것이다
데이터의 수는 1,000이므로 1,000,000회 내에 해결 가능하다
만일 이중 반복문으로 점검한다면 O(N3)회 탐색하게 되어, 시간 초과가 날 것이다
C++ 코드는 다음과 같다
#include <iostream>
#include <string>
#include <vector>
#include <stack>
using namespace std;
// 괄호 삽입 메서드
// 여는 괄호면 삽입
bool checkData(char c) {
return c == '(' || c == '[' || c == '{';
}
// 괄호 짝 점검 메서드
bool checkPair(char c, char top) {
if(c == ')' && top == '(') return true;
if(c == '}' && top == '{') return true;
if(c == ']' && top == '[') return true;
return false;
}
// 괄호 점검 메서드
bool checkBracket(string s) {
stack<int> stk;
for(int i = 0; i < s.length(); i++) {
char c = s[i];
if(checkData(c))
stk.push(c);
else {
// 닫는 괄호가 나온 경우
// stk에 비교할 데이터가 없으면? 이미 잘못된 데이터
if(stk.empty()) return false;
// stk에 데이터가 있으면
// c와 데이터를 비교 해보기
if(checkPair(c, stk.top())) stk.pop();
else return false;
}
}
// 괄호가 모두 빠져나가 stk이 empty라면 true아니면 false
if(!stk.empty()) return false;
return true;
}
int solution(string s) {
int answer = 0;
// 괄호를 회전해야 하므로, length - 1만큼까지 돌린다음 괄호체크
for(int i = 0; i < s.size(); i++) {
string data = s.substr(i, s.size()) + s.substr(0, i);
// data를 돌면서 괄호를 점검하면 됨
// 괄호 점검이 true면 answer을 ++
if(checkBracket(data)) answer++;
}
return answer;
}
3-2. 주식 가격
https://school.programmers.co.kr/learn/courses/30/lessons/42584
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
이 문제는 예전 알고리즘 스터디할 때 Java로 해결했던 문제였다
일반적인 Stack 문제와 달리 입력된 시점을 index로 받아서 얼마 뒤에 가격이 떨어졌는지를 알아야 했다
따라서 index와 value를 저장하는 vector를 생성해 stack에 입력하며 진행해야 하는 조금은 까다로운 문제였다
stack을 활용해 이전에 더 큰 값이 있었는지를 판단하며, 있었다면 answer에 해당 값을 넣어주고
다시 계속 진행하면 되는 것으로 판단했다
최대 들어갈 수 있는 값은 2 ≤ N ≤ 100,000으로 O(N)의 선형 시간 탐색으로 해결 가능하다
#include <iostream>
#include <string>
#include <vector>
#include <stack>
using namespace std;
vector<int> solution(vector<int> prices) {
vector<int> answer(prices.size());
// stack 내에 vector 값을 삽입한다
// 0번은 들어온 시점(index) 1번은 price(value)로 사용한다
stack<vector<int>> stk;
for(int i = 0; i < prices.size(); i++) {
vector<int> now;
now.push_back(i);
now.push_back(prices[i]);
// 비어있거나, 현재 price의 값이 같거나 크다면 그대로 삽입한다
// 현재 값이 같거나 크다는 것은 이전 것이 떨어지지 않았다는 의미
if(stk.empty() || stk.top()[1] <= prices[i]) stk.push(now);
// 비어있지 않으면서, 현재 값이 더 작다면
// 현재 값보다 컸던 이전 값들은 모두 해당 지점에서 떨어진 것과 마찬가지
else {
// 이전 값이 더 크거나 빌 때까지 빼버리면서
// 떨어진 위치를 정답 배열에 입력하자
while(!stk.empty() && stk.top()[1] > prices[i]) {
vector<int> before = stk.top();
answer[before[0]] = i - before[0];
stk.pop();
}
// 다 빼줬으면 now 데이터를 삽입
stk.push(now);
}
}
// 전체 탐색이 끝나면, 스택에 남은 애들을 최종 인덱스에서 빼준다
// 여기 남은 애들은 처음부터 마지막까지 주식 가격이 떨어지지 않은 애들
while(!stk.empty()) {
vector<int> now = stk.top();
answer[now[0]] = (prices.size() - 1) - now[0];
stk.pop();
}
return answer;
}
3-3. 영어 끝말잇기
https://school.programmers.co.kr/learn/courses/30/lessons/12981
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
이 문제도 Java로 해결했었는데, 언제 했는지 기억이 안 난다
요세푸스와 비슷한 문제다
같은 사람들이 계속 반복되는 요세푸스 방식이므로 Queue를 사용하면 해결 가능할 것이라 판단했다
사용한 단어는 다시 사용할 수 없으므로
잘못된 단어를 말한 경우나, 사용한 단어를 다시 사용한 경우를 체크해 답을 출력해야 한다
사용한 단어를 체크하는 방법은 2가지로 고민해 보았다
1. set을 사용해 set의 size가 달라지지 않는 경우에 중복
2. map을 사용해 map에서 해당 값을 가져왔는데, 이미 값이 존재하는 경우 중복
map에 익숙해져야 하니까 map과 count를 활용해 풀어보았다
이 방법은 선형 탐색 O(N) 내로 해결 가능하다
#include <string>
#include <vector>
#include <iostream>
#include <queue>
#include <map>
using namespace std;
// 중복값 체크할 map 생성
map<string, int> checkMap;
bool checkWord(string s1, string s2) {
return s1[s1.length() - 1] == s2[0];
}
bool duple(string s) {
if(checkMap.count(s) > 0) return true;
++checkMap[s];
return false;
}
vector<int> solution(int n, vector<string> words) {
vector<int> answer = {0, 0};
queue<int> q;
// 사용자를 q에 1부터 n까지 집어 넣음
for(int i = 1; i <= n; i++) {
q.push(i);
}
// 1번은 틀릴 수 없으므로
// 맨 뒤에 입력해주자
q.pop();
q.push(1);
duple(words[0]);
// words의 길이만큼 순회하며 진행
// 단 이전 글자와 비교하기 위해 처음은 생략함(index error 배제)
for(int i = 1; i < words.size(); i++) {
string before = words[i-1];
string now = words[i];
// 지금 순서
int peopleNum = q.front();
// 이전 단어 맨 뒷 글자와 현재 단어 맨 앞 글자가 다르면
// 또는 중복 단어를 말했으면
// 끝말잇기 끝
if(!checkWord(before, now) || duple(now)) {
answer[0] = peopleNum;
answer[1] = i / n + 1;
return answer;
}
q.pop();
q.push(peopleNum);
}
return answer;
}
3-4. 베스트 앨범
이 문제는 Java에서 2개의 Map을 활용해 해결했던 문제였다
단순히 Queue나 Stack을 하나만 사용해서는 해결할 수 없을 듯했다
deque를 사용하면 더 편리하지 않을까 생각하긴 했다
맨 뒤에 있는 값보다 크면 그냥 뒤에 삽입하면 되고,
아니면 앞에 값부터 비교하며 더 작으면 앞의 값을 임시로 다른 Stack에 담은 다음에
일치하는 부분에 넣은 뒤 Stack 내용을 싹 빼면서 다시 Deque에 옮겨주면 된다
일단 분류 자체가 해시고, 우선순위 큐 등을 C++로 구현하는 연습을 해보지 않아서
추후 과제로 남겨두고자 한다
정렬도 꽤 추가되어 있는 문제라 우선순위 큐(Priority Queue)를 학습한 뒤 해결하면 편리할 것이라 생각된다
4. Java에서의 Stack
Stack은 우선 Vector class를 상속받는다
Vector class는 추후에 까보도록 하자...
4-1. push()
Stack 내의 push 메서드는 다음과 같다
public E push(E item) {
addElement(item);
return item;
}
그럼 addElemet는 무엇인가?
public synchronized void addElement(E obj) {
modCount++;
add(obj, elementData, elementCount);
}
간단하게 살펴보면
sychronized 키워드는 동기화를 위해 thread-safe 한 메서드를 만들기 위해 사용되었다
modCount는 배열 수정 횟수를 측정한다
AbstactList 클래스와 그 하위 클래스에서 주로 사용되며, fail-fast iterator를 구현할 때 사용된다고 한다
(이건 추후에 살펴봐야겠다)
그럼 add 메서드는 무엇인가?
private void add(E e, Object[] elementData, int s) {
if (s == elementData.length)
elementData = grow();
elementData[s] = e;
elementCount = s + 1;
}
만일 데이터의 길이가 끝까지 도달했으면 grow()함수를 통해 배열 사이즈를 늘린다
private Object[] grow(int minCapacity) {
int oldCapacity = elementData.length;
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
capacityIncrement > 0 ? capacityIncrement : oldCapacity
/* preferred growth */);
return elementData = Arrays.copyOf(elementData, newCapacity);
}
private Object[] grow() {
return grow(elementCount + 1);
}ArrayList와 동일한 방식으로 해당 사이즈를 늘려가는 모습을 볼 수 있다
그리고 s번 인덱스에 해당 값을 입력하고, 원소의 개수를 늘려준다
이게 Stack이 데이터를 입력하는 방법이다
4-2. pop()
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}우선 peek을 진행한 뒤 길이 마지막 원소를 제거하고, 해당 값을 반환해준다
removeElement는 다음과 같이 동작한다
public synchronized void removeElementAt(int index) {
if (index >= elementCount) {
throw new ArrayIndexOutOfBoundsException(index + " >= " +
elementCount);
}
else if (index < 0) {
throw new ArrayIndexOutOfBoundsException(index);
}
int j = elementCount - index - 1;
if (j > 0) {
System.arraycopy(elementData, index + 1, elementData, index, j);
}
modCount++;
elementCount--;
elementData[elementCount] = null; /* to let gc do its work */
}인덱스 최댓값 처리, 0 미만 값 처리가 진행된다
System.arraycopy 메서드는 배열을 보가하고, 뒤에 남은 값들을 이동시켜주는 역할을 한다
그런데 스택은 중간 값이 사라지는 경우가 없어 해당 구문이 뒤의 값을 앞으로 옮겨주는 부분이 필요한지는 의문이다
하지만 만들어두신 분들이 필요한 경우가 있으니까 만드셨겠지...?
마지막에 값을 null로 바꾸고 가비지 컬렉터에 맡기는 부분이 있는건 신기했다
4-3. peek()
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}peek의 구조는 이렇게 되어있다
size가 0이면 비었다는 오류를 반환하고, 아니면 해당 index의 원소를 반환한다
public synchronized E elementAt(int index) {
if (index >= elementCount) {
throw new ArrayIndexOutOfBoundsException(index + " >= " + elementCount);
}
return elementData(index);
}
반환 값은 elementData배열의 index 값을 반환한다
5. Java에서의 Queue
Queue는 우선 Collection을 상속받는 인터페이스이다
해당 Queue를 상속받는 구현체가 꽤 많은 것 같다

Queue의 구현체 중 자주 사용하는 LinkedList를 기준으로 살펴보자
5-1. offer(), add()
public boolean offer(E e) {
return add(e);
}offer는 이렇게 구현되어 있다
나는 주로 offer를 사용했는데 미묘한 차이가 있다
우선 add는 Collection에서 정의된 메서드이고, doffer는 Queue에서 정의된 메서드이다
add는 추가가 불가능한 경우 예외를 던지고, offer는 false값을 반환한다
또한 queue에서 offer를 제공하며, queue 동작을 더욱 명확히 해주므로 offer를 사용하는 것이 좋아 보인다
그럼 add 메서드는 어떻게 구성되어 있는가?
public boolean add(E e) {
linkLast(e);
return true;
}여기까지 왔으면 귀찮아도 linkLast까지 들어가보자
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}linkedList는 기본적으로 노드들의 연결을 통해 구성된다
이 부분은 따로 정리가 필요한 부분이라 일단 패스한다
final Node<E> l = last; 마지막 노드를 가져오고
final Node<E> newNode = new Node<>(l, e, null); 새로운 노드에 e 값을 넣고 생성한다
last = newNode; 마지막 값을 현재 노드로 설정한다
if(l == null ) first = newNode 마지막 값이 없을 경우 맨 앞을 현재 값으로 설정해준다
else l.next = newNode;마지막 값이 있다면, 해당 값의 다음으로 연결을 해준다
size++;을 통해 크기를 늘려주고, modCount++;을 통해 수정 횟수도 늘려준다
생각보다 구조가 간단하다 그럼 출력은 어떻게 해줄까?
5-2. remove(), poll()
보통 poll()을 사용해 값을 가져온다
remove 메서드가 있는 것도 까보고 처음 알았다
remove()는 q에 가져올 값이 없을 때 NoSuchElementException 예외를 발생시키지만, poll()은 null값을 반환해준다
remove()는 다음 구조로 진행된다
public E remove() {
return removeFirst();
}public E removeFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
return unlinkFirst(f);
}
poll()을 기준으로 살펴보자
public E poll() {
final Node<E> f = first;
return (f == null) ? null : unlinkFirst(f);
}null을 반환하거나, unlinkFirst(f)를 수행한다
private E unlinkFirst(Node<E> f) {
// assert f == first && f != null;
final E element = f.item;
final Node<E> next = f.next;
f.item = null;
f.next = null; // help GC
first = next;
if (next == null)
last = null;
else
next.prev = null;
size--;
modCount++;
return element;
}element에 f의 데이터 값을 저장한다
next에는 f의 다음 값을 저장한다
f.item = null;, f.next = null; 현재 노드의 연결을 해제한 뒤 값을 없애고 가비지 컬렉터에 맡긴다
first = next;로 가장 앞의 값을 현재의 다음 값으로 변경해준다
if (next == null) last = null; 만일 다음 값이 없으면, last를 null로 설정한다
else next.prev = null; 만일 값이 있으면, 그 다음 값의 이전(즉 지금 값)을 null로 설정해 연결을 해제한다
size--; 전체 사이즈를 줄이고 modCount++;로 수정 횟수를 늘려준다
return element; 현재 데이터 값을 반환해준다
우리는 단순히 poll()을 사용하지만 안에서는 연결 해제의 많은 과정을 우리 몰래 거치고 있었다...!
5-3. peek()
peek()은 특별히 연결된 부분은 없다
public E peek() {
final Node<E> f = first;
return (f == null) ? null : f.item;
}first 값을 가져와서 null이면 null을 반환하고 아니면 first의 item, 즉 데이터를 반환한다
마무리
스택과 큐에 대해 정리를 간단하게 진행해 보았다
스택과 큐는 삽입(push, offer), 삭제(pop, poll), 조회(peek)에서 O(1)의 시간 복잡도를 가진다
코딩 테스트에서 많은 N값이 주어질 경우,
그리고 입력 값을 출력하여 사용할 때 그 순서가 뒤, 또는 앞으로 고정된 경우에 사용을 고려해 볼 만 하다
Java에서 스택과 큐를 처음 들여다 보았다
꽤나 직관적으로 구성되어 있어 이해가 편했다
'알고리즘 > 스터디' 카테고리의 다른 글
| [코딩 테스트 합격자 되기 C++ 스터디] STEP 5. 집합 (0) | 2024.08.16 |
|---|---|
| [코딩 테스트 합격자 되기 C++ 스터디] STEP 4. 트리 (0) | 2024.08.03 |
| [코딩 테스트 합격자 되기 C++ 스터디] STEP 3. 해시 (0) | 2024.07.26 |
| [코딩 테스트 합격자 되기 C++ 스터디] STEP 1. 시간 복잡도 (0) | 2024.07.07 |
